집합? ㅎㅎ 집합 원소 부분집합 원소나열법 조건제시법 벤다이어 그램~ ㅋㅋ
중학교 1학년 학생 수학 개념이 안 잡힌다기에 ㅎㅎ 잠시 알려주고 왔어요 그런데~
외국에서는 집합을 뭐라고 부르는지 궁금하더군요
위키 백과를 기준으로 찾아 보았어요 ㅎㅎ
1. 집합 / set / 集合（しゅうごう) / 集合（或簡稱集）
<
집합은 서로 구별되는 대상들을 순서와 무관하게 모은 것이다. 이때 집합에 속하는 각각의 대상들을 원소라고 한다.
>
영어는
<
A set is a collection of distinct objects, considered as an object in its own right. Sets are one of the most fundamental concepts in mathematics.
>
일본어는
<
集合（しゅうごう、英: set, 仏: ensemble, 独: Menge）とは、大雑把に言えばいくつか（有限または無限）の「もの」からなる「集まり」である。集合に含まれる「もの」のことを元（げん、element; 要素）という。
>
중국어는
<
集合（或簡稱集）是基本的數學概念，它是集合論的研究對象。最簡單的說法，即是在最原始的集合論─樸素集合論─中的定義，集合就是「一堆東西」。集合裡的「東西」，叫作元素。
>
2. 원소 / element / 元（げん) / 元素 ...
...
흠~ 그렇군 하면서 보고 있는데~... 집합 기호에서 부분집합에서 갑자기 의문이 생기네여
문제는 여기 입니다 ^^ < ⊂ 과 ⊆ >
허걱 이건 다른건가요?
우선 영어부분을 참조하니 부분집합을 ⊆ 로 표기하네여
<
Subsets
If every member of set A is also a member of set B, then A is said to be a subset of B, written A ⊆ B (also pronounced A is contained in B). Equivalently, we can write B ⊇ A, read as B is a superset of A, B includes A, or B contains A. The relationship between sets established by ⊆ is called inclusion or containment.
If A is a subset of, but not equal to, B, then A is called a proper subset of B, written A ⊊ B (A is a proper subset of B) or B ⊋ A (B is proper superset of A).
Note that the expressions A ⊂ B and B ⊃ A are used differently by different authors; some authors use them to mean the same as A ⊆ B (respectively B ⊇ A), whereas other use them to mean the same as A ⊊ B (respectively B ⊋ A).
Example:
-
- The set of all men is a proper subset of the set of all people.
- {1, 3} ⊊ {1, 2, 3, 4}.
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4}.
The empty set is a subset of every set and every set is a subset of itself:
-
- ∅ ⊆ A.
- A ⊆ A.
An obvious but useful identity, which can often be used to show that two seemingly different sets are equal:
-
- A = B if and only if A ⊆ B and B ⊆ A.
>
일본어는 ⊆ / ⊂ 같이 쓰네여
<
>
중국어 설명을 보니... ⊆ / ⊂ 를 구별을 해 놓았고요
<
子集与包含关系
定义
集合A，B，若∀a∈A，有a∈B；A⊆B。则称A是B的子集，亦称A包含于B，或B包含A，记作A⊆B。
若A⊆B，且A≠B，则称A是B的真子集，亦称A真包含于B，或B真包含A，记作A⊂B。
基本性质
- 包含关系“⊆”是集合间的一个非严格偏序关系，因为它有如下性质：
- 自反性：∀集合S，S⊆S；（任何集合都是其本身的子集）
- 反对称性：A⊆B且B⊆A ⇔ A=B；（这是证明两集合相等的常用手段之一）
- 传递性：A⊆B且B⊆C ⇒ A⊆C；
- 真包含关系“⊂”是集合间的一个严格偏序关系，因为它有如下性质：
- 反自反性：∀集合S，S⊂S都不成立；
- 非对称性：A⊂B ⇒ B⊂A不成立；反之亦然；
- 传递性：A⊂B且B⊂C ⇒ A⊂C；
- 显然，包含关系，真包含关系定义了集合间的偏序关系。而Ø是这个偏序关系的最小元素，即：∀集合S，ØS；且若S≠Ø，则ØS，（空集是任何集合的子集，是任何非空集合的真子集）
举例
-
- 所有男人的集合是所有人的集合的真子集。
- 所有自然数的集合是所有整数的集合的真子集。
- {1, 3} ⊂ {1, 2, 3, 4}
- {1, 2, 3, 4} ⊆ {1, 2, 3, 4}
>
왜 한국에서만 ⊆ / ⊂ 를 구별하지 않는지 궁금해 졌습니다
이공계에 강한 나라가 어디 있더라 ㅎㅎ 생각해 보니
독일이 있더군요 독일어는 모르지만 찾아보니 독일도 구별을 하는군요
<
Teilmenge [Bearbeiten]
→ Hauptartikel: Teilmenge
Wenn alle Elemente in einer Menge A auch in einer zweiten Menge B enthalten sind, so nennt man Menge A eine Teilmenge von Menge B. Die Menge B enthält dann mindestens so viele Elemente wie die Menge A. Für Teilmengen wird das Zeichen 
verwendet.
Formal: Es gilt 
, wenn aus 
folgt, dass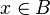 
ist.
Nach dieser Definition ist jede Menge auch Teilmenge von sich selbst: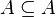 
. Der Unterstrich in dem Zeichen soll das andeuten, indem er an ≤ erinnert. Eine echte Teilmenge von B ist eine Teilmenge, die nicht B selbst ist, geschrieben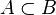 
.
Hinweis: Die Notation der Teilmengenrelation ist uneinheitlich, die beiden folgenden Möglichkeiten sind heute üblich, wobei die erste der ursprünglich von Bertrand Russell (vgl. Principia Mathematica) eingeführten entspricht:
- steht für „Teilmenge“,
für „echte Teilmenge“
- steht für „Teilmenge“,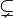
für „echte Teilmenge“.
>
부분 집합을 나타내는 기호 ⊆ / ⊂ 는 분명 차이가 있어 보이네여
제가 수학을 전공한 사람이 아니어서 그 내용을 구별 할 수 없네여 ^^
찾다 알 수 없어 네티즌 여러분의 조언을 구합니다~ 정확한 구별 방법을 좀 알려주세요~